قد يكون عباقرة الرياضيات قد حلوا مشكلة الجبر ”المستحيلة“

لقرون عديدة، ظل سؤال بسيط يطارد علماء الرياضيات: هل يمكن حل جميع المعادلات، مهما كانت درجتها؟ منذ القرن التاسع عشر، بدا أن الإجابة هي ”لا“ قاطعة.

في المدرسة، غالبًا ما نتعلم كيفية ضرب وتفكيك كثيرات الحدود مثل (x² + 2x + 1)، أو (x² – 1). في الحياة الواقعية، تصبح هذه المعادلات معقدة للغاية بسرعة كبيرة. وفي حين أنه يمكن حل المعادلات التربيعية والتكعيبية والرباعية باستخدام صيغ صريحة، لا توجد صيغة عامة للمعادلات التي تزيد درجتها عن أربعة، وعادةً ما يقتصر علماء الرياضيات على إيجاد حلول تقريبية للمعادلات التي تتجاوز درجتها أربعة. هذه الحقيقة هي أساس كل مناهج الجبر المتقدم.

ومع ذلك، قدم باحثان مؤخرًا نهجًا جديدًا ومفاجئًا للتغلب على هذا المأزق. من خلال الاستفادة من الهندسة والتحليل التوافقي وجرعة كبيرة من الإبداع، يزعم هذان الباحثان أنهما ابتكرا طريقة لحل بعض هذه المعادلات المعقدة باستخدام أدوات مختلفة تمامًا عن الطرق التقليدية.

شراكة غير متوقعة - عالم رياضيات ”مهرطق“ وخبير خوارزميات:

في قلب هذا الاكتشاف يوجد نورمان وايلدبرغر، أستاذ الرياضيات الفخري في جامعة نيو ساوث ويلز في أستراليا، المعروف بآرائه النقدية حول الأسس التقليدية لمجاله. تقاعد وايلدبرغر في عام 2021 بعد أن درّس في الجامعة منذ عام 1990، ويدعو إلى إلغاء مفاهيم اللانهاية والأعداد غير العادية في مجالات معينة من الرياضيات. وقد أكسبه موقفه الراديكالي لقب ”الرياضي المهرطق“.

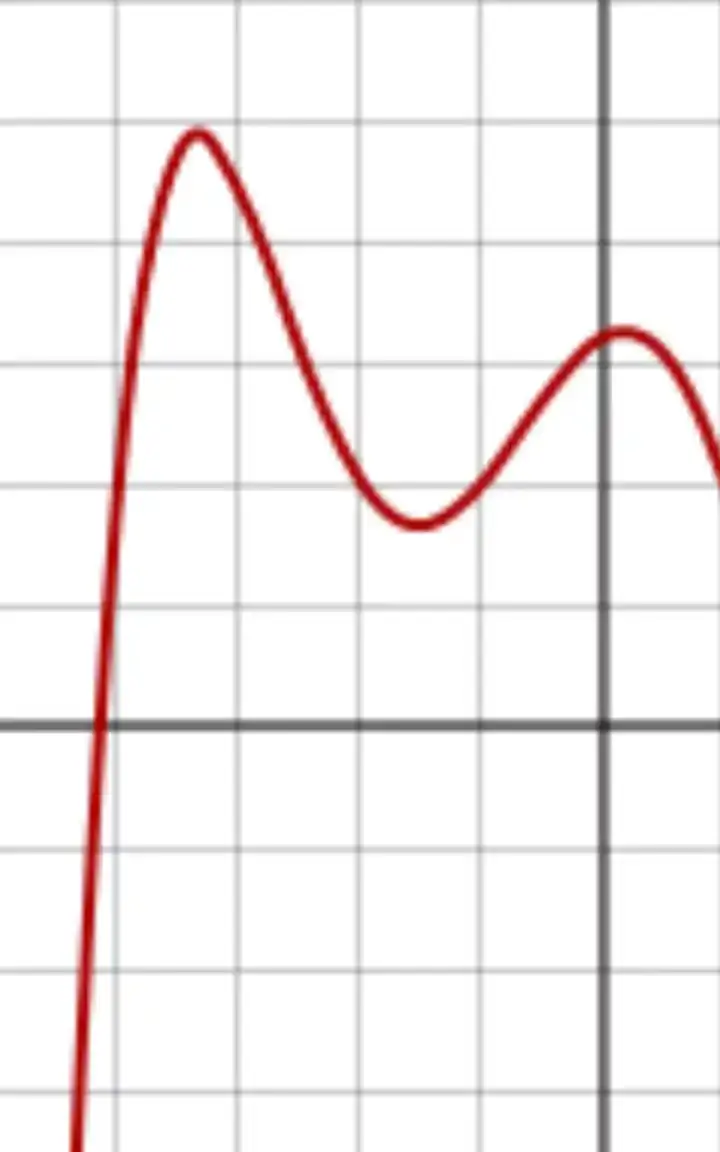
الخط البياني لكثير حدود من الدرجة الخامسة. من المعروف أننا لا نستطيع إيجاد حلولها

يعمل معه دين روبين، عالم حاسوب عمل في مختبرات بيل وكارنيجي ميلون، وهو الآن مدير تقني في صندوق تحوط متخصص في الخوارزميات. بدأت تعاونهما على YouTube، حيث ينشر وايلدبرغر مقاطع فيديو تعليمية منذ عام 2021، بهدف معالجة ”مشكلة مستعصية“: إيجاد طريقة جديدة لحل كثيرات الحدود العامة. أثار ذلك فضول روبين، الذي تابعه عن كثب. بعد عامين و 41 مقطع فيديو، لم يكن وايلدبرغر قد كتب بعد ورقة علمية، لذلك أخذ روبين على عاتقه تنظيم نتائج بحثهما في منشور مشترك.

السلاح السري - الأعداد الكاتالونية:

لتجاوز العقبات التقليدية، يعتمد الفريق على بنية رياضية مألوفة للهندسيين وعلماء الحاسوب، وهي الأعداد الكاتالونية.

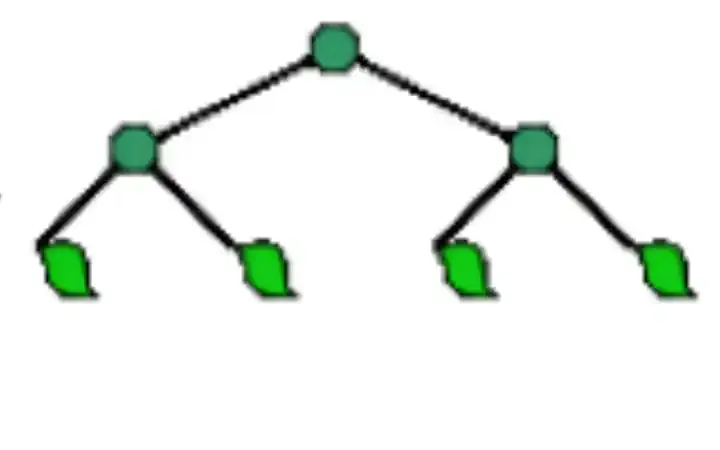
استخدام الأعداد الكاتالونية في تخطيط الأشجار الثنائية

الأعداد الكاتالونية هي أعداد طبيعية تنتج عن مجموعة من السيناريوهات الرياضية المختلفة، ويمكن العثور عليها من خلال القيام بتقطير مثلث باسكال لمعاملات كثيرات الحدود. تساعد هذه الأعداد علماء النظريات البيانية وعلماء الحاسوب على تخطيط بنى البيانات التي تسمى الأشجار من خلال إظهار عدد التراتيب المختلفة للأشجار التي يمكن إجراؤها ضمن وسطاء معينة. تقوم أيضًا بتحديد عدد الطرق التي يمكنك من خلالها تقسيم مضلع من أي حجم إلى عدد معين من المثلثات.

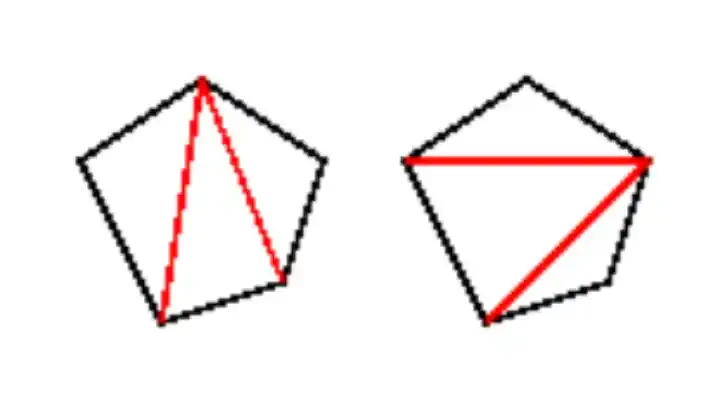
وتستعمل أيضًا في تقسيم المضلعات إلى مثلثات

تتميز هذه الورقة البحثية بطابع تعليمي، حيث تقرأ وكأنها فصل من كتاب مدرسي جيد. يحدد المؤلفان مصطلحاتهما، ثم يبنيان حججهما واحدة تلو الأخرى لتشكل صورة كاملة. ويقترح الباحثان أن هذه الأعداد يمكن أن تكون أيضًا أساسًا هندسيًا وتركيبيًا لإعادة بناء حلول لمعادلات كثيرات الحدود المعقدة. من خلال استكشاف هذا المفهوم، طورا بنية رياضية جديدة: ”المصفوفة الكاتالونية الفائقة“، التي تحتوي على الأعداد الكاتالونية الكلاسيكية بالإضافة إلى امتداد يشمل أعدادًا أخرى تستوفي شروط حل كثيرات الحدود. وكل هذا مضمّن في مصفوفة تسمى Geode، وهي أداة ترسم الحلول بطريقة جديدة.

ربط الجبر والهندسة:

في حين تسعى الطرق التقليدية إلى التعبير عن جذور كثيرات الحدود من خلال الجذور أو الدوال المتسامية (transcendental)، يقدم وايلدبرغر وروبين نهجًا أكثر هندسية، يستند إلى منطق التراتيب والتماثلات.

وهما يعتقدان أن التحدي لا يكمن في المعادلة نفسها، بل في الطريقة التي نحاول بها حلها. من خلال رفض بعض المفاهيم ”غير البناءة“، مثل الجذور من الدرجة n أو اللانهاية، يركزان على أدوات أكثر واقعية مثل المتسلسلات، التي تسمح بمعالجة العبارات الرمزية دون الحاجة إلى إعطاء قيمة دقيقة لكل حدّ.

وكتبا في ورقتهم البحثية: ”توفر المتسلسلات بدائل جبرية وتوافقية صريحة للتوابع التي لا يمكن تقييمها بشكل ملموس. وينبغي أن تلعب دورًا أكثر مركزية في الرياضيات الحديثة“.

الردود والتوقعات:

ورقتهما البحثية، التي نُشرت في مجلة American Mathematical Monthly، وهي مجلة ذات اهتمام واسع، محكّمة من قبل الأقران تابعة لجمعية الرياضيات الأمريكية، دقيقة وتعليمية. يتم تقديم كل مفهوم بعناية، والتعريفات دقيقة، والحجج مبنية بشكل منهجي. النبرة تشبه إلى حد كبير نبرة الكتب الجامعية، ما يجعل عملهما في متناول أي شخص لديه أساس متين في الرياضيات.

يبقى أن نرى كيف ستكون ردود فعل المجتمع العلمي. قد لا تلقى الطبيعة غير التقليدية للنهج وشخصية وايلدبرغر المتمردة قبولًا في بعض الأوساط الأكاديمية. ومع ذلك، فإن الأفكار موجودة، وكذلك الإمكانات.

في منتدى Hacker News، يشارك روبين قائلاً: ”عندما قال وايلدبرغر إنه سيحل المعادلة كثيرات الحدود العامة، اعتقدت أنه يمزح، لأن الجميع ”يعرف“ أنه لا يمكننا تجاوز الدرجة الرابعة. لكنه كان جادًا. بعد عامين، لم يكن قد كتبها بعد، لذا كتبت مسودة وأرسلتها إليه، والتي تطورت إلى هذه الورقة البحثية“.

نحو ثورة هادئة؟

لا يدعي هذا العمل أنه يحل كل شيء. فهو لا يتعارض مع النتائج الكلاسيكية، لا سيما تلك التي أثبتها نظرية غالوا، والتي تثبت أنه من المستحيل إيجاد صيغة واحدة بواسطة الجذور لجميع الدوال من الدرجة الأعلى من أربعة.

لكن حيث تستسلم الطرق التقليدية، يقترح وايلدبرغر وروبين مسارًا آخر. نهجهما بناء ودقيق ويمكن تطبيقه في مجالات مثل التشفير والتحليل الرمزي وتصميم الخوارزميات.

بفضل ”الجيود الكاتالوني الفائق“ الخاص بهما، فإنهما يخترقان حصنًا رياضيًا طالما اعتُقد أنه منيع. هناك شيء واحد مؤكد: عملهما يثير بالفعل العديد من الأسئلة. وربما، بمرور الوقت، سينخرط باحثون آخرون في هذا العمل لتعميق أو تحدي نتائجهما.